Estadística I

Es una herramienta de gran utilidad para el análisis de datos, a partir de los cuales se pueden encontrar patrones que describen el comportamiento de algún fenómeno, y generar hipótesis sobre el posible curso que seguirá.

Fundamentos de la estadística y el muestreo. El objetivo de la estadística es reunir información cuantitativa sobre grupos, series de hechos, individuos, etcétera.

Ramas de la estadística. Descriptiva: Presenta y clasifica los datos obtenidos de la población (describe la población). Inferencial: Plantea y da solución a problemas específicos estimando resultados con base en los datos existentes.

Teoría de muestreo. Población: Universo de datos existentes dentro de una categoría de interés. Muestra: Es un subconjunto de la población que representa su compartimiento general y facilita la obtención de información. *Error muestral*. Al tomar una muestra de una población se genera un cierto error, pues por más representativa que sea la muestra siempre habrá un ligero sesgo.

Métodos de muestreo Aleatorio: Se toman individuos al azar. Estratificado: Se crean categorías típicas de elementos. Conglomerados: Grupo de elementos con características en común que se eligen de forma aleatoria.

Organización de datos. ¿Que son los datos? Representan la información que ofrece conocimiento preciso y concreto. Su organización es importante para un análisis adecuado y su representación gráfica. ¿Cómo se pueden organizar? Con una tabla de frecuencias, estás son una herramienta que posibilita organizar los datos de una muestra estadística, agrupándolos en intervalos y clases para facilitar su análisis.

Representación gráfica. ¿Que es? La representación gráfica de datos es parte fundamental de cualquier análisis estadístico ( el tipo de representación utilizado depende de la clase de datos a evaluar). Datos cualitativos: Son datos que generalmente expresan opiniones, motivaciones o información que no puede expresarse con cifras. •Graficas de barras •Graficas de pastel o circulares. Datos cuantitativos: Son datos que expresan cantidades concretas y pueden utilizarse para elaborar estudios estadísticos»duros». •Histogramas

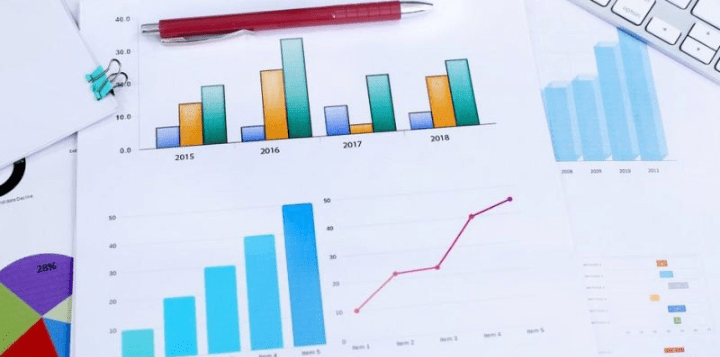
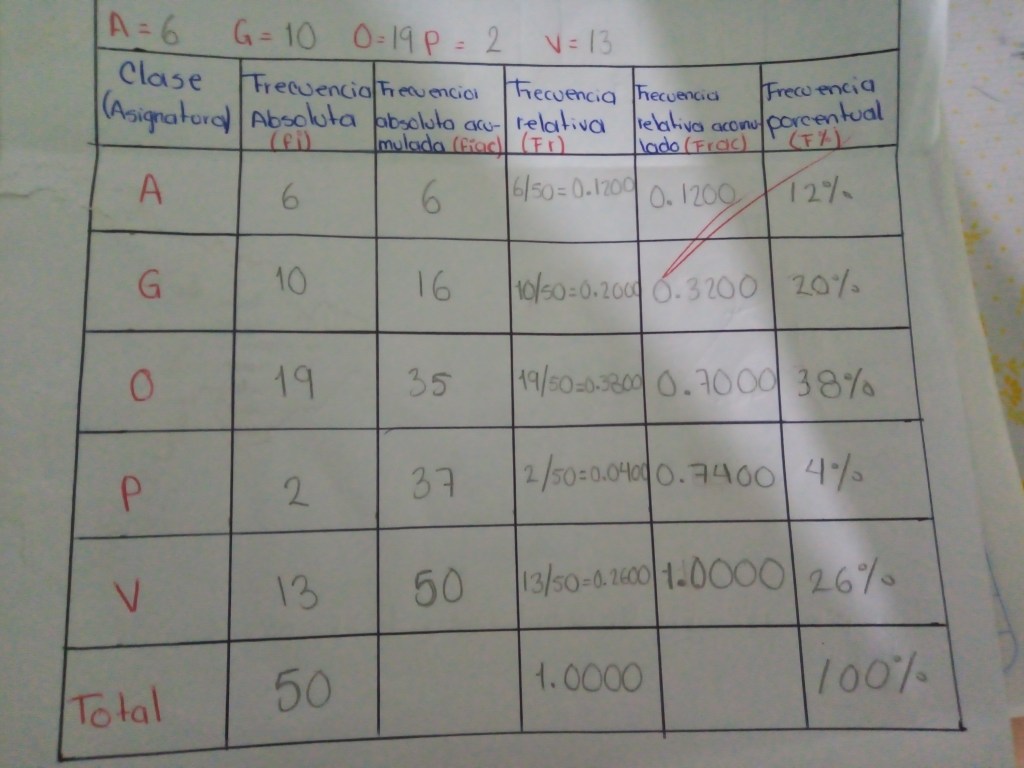
«Elementos de la tabla de frecuencias». Intervalo de clase: Es una división arbitraria para distinguir entre un conjunto de valores y los demás. Frecuencia relativa: Es el porcentaje que representa una clase dentro de la muestra. Frecuencia acomulada: Es el porcentaje de la muestra que representa todas las clases acomuladas hasta cierto intervalo.

Medidas de tendencia central pt. 1. Media: se obtiene sumando todos los valores y dividiendo el resultado entre el número total de datos. Mediana: valor que se ubica en la mitad de la distribución cuando los datos se acomodan. Moda: valor que más se repite en una serie de números. Media geométrica: se ocupa para calcular porcentajes a lo largo del tiempo. Medidas de tendencia central pt. 2 Promedio móvil: Es un procedimiento de cálculo para organizar y crear pronósticos a lo largo del tiempo. Media armónica: son números inversos a la media aritmética. Deciles, cuartiles y porcentiles: 25% -Deciles: los datos se dividen en 4 partes iguales. 10% -Cuartiles: Los datos se dividen en 10 partes iguales. 1% -Porcentiles: Los datos se dividen en 100 partes iguales.

Medidas de variabilidad o dispersión parte 1. Rango: es la diferencia entre el dato mayor y el menor de un conjunto de datos. Desviación: diferencia que hay entre cada uno de los datos y la media del conjunto de datos. Desviación estándar: Es un índice que demuestra cuánto se diferencia una puntuación común y la media de un grupo de puntuaciones. Varianza: es la media del cuadrado de las desviaciones de la distribución de datos. medidas de variabilidad o dispersión parte 2. Asimetría: Sirve para comparar conjunto de datos respecto de la media en poblaciones o muestras. Curtosis: es la media de una distribución e indica los datos que tienden a la derecha o izquierda de una curva. Coeficiente de variación: ayuda a observar qué tanto varía la curva respecto de la distribución de los datos que se acercan a la media.

Probabilidad parte 1. Suceso: Resultado de un experimento aleatorio. Experimento aleatorio: El resultado depende del azar. Espacio muestral: Posibles resultados de un experimento. Esperanza matemática: Es el valor esperado de un fenómeno. Diagrama de árbol: Se utiliza para representar probabilidades. Tipos de probabilidad: Clásica: Probabilidad de que suceda un evento. Subjetiva: Se basa en la experiencia individual Frecuencial: Se basa en los resultados de estudios previos. Probabilidad parte 2. Permutaciones: Agrupaciones en los que si importa el orden de los objetos. Combinaciones: No importa el lugar o la posición de los elementos.

Tipos de eventos: Independientes: Los eventos no dependen de ningún resultado o proceso. Dependientes: El resultado del segundo evento depende del primero y la probabilidad cambia. Condicionales: Los eventos A y B son detonantes uno del otro.